Reducing project durations
General
Every project consists of tasks and these in turn have a finite duration consisting of labour, equipment and materials.
When we look at ways to reduce the overall length of a project the easy view is to throw more resources at it.
This simplistic view does not consider the limitations and issues of increasing the 3 resources.
There will be limitations to how many people you can put onto one job, for example:
- Not all workers are highly productive which will reduce the effective output per man.
- Space may be limited reducing worker efficiency.
- People may have personal issues which reduces their efficiency to work together.
There are similar problems for equipment:
- Extra equipment usually means extra labour.
- There may not be enough skilled labour for the machinery to run.
- Equipment takes up space which may not be available.
Similarly for materials.
- These may not be readily available.
- Storage space may be limited etc.
Even with these issues there are many advantages in trying to reduce a projects lifespan.
- Projects are funded with borrowed money which is costing the project interest every day.
- The shorter the project the less the interest costs.
- The overheads of running projects over a year are reduced per project if you carry out more.
- Carrying out more projects speedily to a high standard increases the company reputation and more work ensues.
- Accepting poor schedules encourages poor performance in other areas.
There are two key ways to reduce a project schedule.
These are ‘task splitting’ and ‘crashing’.
Task splitting
The aim here is to take a large task and to split it down into two or more smaller tasks each of which could start ahead of the completion of the previous one. This can happen more often than you think.
In an ideal world the work break down structure will already go down to the lowest available task.
If this were the case there would be no tasks to split and every task precedence would be sorted.
When you examine a task and split it you are not adding more resource merely adjusting the overlap of the individual smaller tasks.
In addition, when you modify the start times of the individual smaller tasks the overall duration of the original task remains the same.
There are a few things to consider when choosing a task to split and how to do it most efficiently.
- The task you are considering for ‘splitting’ must be on the critical path otherwise you cannot reduce the overall project duration.
- Tasks after splitting should not all run in series.
- The tasks after splitting cannot use the same resource at the same time.
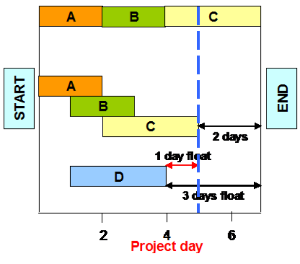
If we look at the simple example in the diagram we have a single task shown as ‘A’ ‘B’, and ‘C’ in one block at the top.
This single task is also critical as it goes from beginning to end.
We can split these into the individual tasks ‘A’ ‘B’, and ‘C’.
Having considered these activities very carefully we decide that task ‘B’ can start 1 day after task ‘A’ has begun.
Similarly, task ‘C’ can begin 1 day after the start of task ‘B’.
If we adopt this new structure then the critical path still ends at the end of task ‘C’ but it is now shortened by 2 days.
Notice that the durations of tasks ‘A’ ‘B’, and ‘C’ have not changed.
Also, within the schedule we have task ‘D’ (in blue). This task originally had a total float of 3 days. Due to the reduction in the overall project time its float (that is, total float) has been cut to 1 day.
Note that when the schedule is more complex you will need to take other aspects into consideration.
- The original critical path will be shortened but there is no guarantee that it will remain the critical path. Indeed, if the float of a task is less than the original critical path reduction that task will become critical.
For example, if we have:
A task ‘X’ with total float = 16 days
Project reduction = 20 days
The total float of task ‘X’ becomes 16 – 20 = 0 days
Note that it can’t be -4 days. Once a task gets to total float = zero it is on the critical path.
Be wary when dealing with critical paths. There may be more than one.
If there is more than one and you carry out task splitting on only one task of one of the critical paths then the overall project duration will not change as it will be governed by the remaining critical path.
In this case if you want to reduce the overall project you must carry our task splitting on two tasks. One from each critical path.
The path that is shortened the least will remain as the critical path.
Once you have done this once you will need to recalculate the critical path before deciding on the next pair of tasks to split.
When you have split any tasks, particularly a pair in two critical paths make sure that the 3 point rule considered above has not been broken before going through the cycle again.
Crashing
This is different to task splitting. Here we add extra resource to a task to increase its rate to completion.
The resource that is added will be the ‘rate determining’ resource. This is usually people but could be equipment or material.
The simplistic view is ‘double the workers and half the duration’. This is clearly too optimistic a view.
For any task, there will always be a duration that you cannot go below.
For example, it may be physically impossible for a number of people to work within the same space.
Some people just don’t get on with others very well and lower overall working efficiency. Not everyone works to the same performance level so various combinations can vary the productivity.
Another common resource to add is extra equipment. Again extra equipment can be hampered by room for working or a lack of suitably qualified staff to work it.
It may be that materials are rate determining. If material is limited to a particular level that may not be enough to maintain high productivity.
It could be that increasing the rate of raw material availability would require excessive costs. This may not be a problem for a task not on the critical path.
We know that not every person will work to the same level of performance. When you consider the group for a particular task they can be considered as a core group of workers that you would consider as your standard. These would be your best people.
Let us assume that you have a group of 5 people considered your best. If you could run every task based using this resource your productivity would always be at its best. You might base your estimates of duration on the use of a ‘best group’.
The duration will = quantity of work / daily productivity of the ‘best’ group
For example, if you needed to lay 9,000 bricks and your best people could lay 300 per day then the duration = 9000 / (300 x 5) = 6 project days.
However, you can never maintain a perfect group of workers. You will have different people on different tasks.
When you add resource to a task in order to ‘crash’ it you may well be diluting the productivity due to adding a worker whose output may be only 200 bricks per day.
Here, by dilution, we mean reducing the effective output per man.
For example, if we have 5 men who can lay 300 bricks each per day the output = 5 x 300 = 1500 bricks.
If we add one person who can only lay 200 bricks per day the total will be 1500 + 200 = 1700.
These have been laid by 6 men so the new rate of brick laying per man per day = 1700 / 6 = 283 /man/day.
When any sort of resource is added to a task there will be a cost involved.
The project manager must assess the benefits of reducing a task’s duration and weigh this against the extra cost in doing so.
When to crash
Before you can crash any tasks there must be a certain items in place.
- You must have a schedule of all tasks together with their total floats.
- You must know the durations of each task
- There must be financial information available that will allow you to reach a cost for reducing a task by 1 day.
- You must know the total fixed costs per day.
With this data you can then consider the crashing strategy.
- Examine the critical paths and their tasks. You want to begin with the task that costs the least to ‘crash’. That is the one that has the lowest penalty per day.
- Cut the task duration by one day and then revise the critical path and subtract 1 day from each of the task total floats.
- Be careful it may not always be necessary to reduce the floats. Identify the resultant critical path.
- You will then need to calculate the cost and the fixed costs saved. The cost benefit will also be the project cost saving.
- If the cycle is then repeated the new cost saving can be added to the first to get the total project saving and so on.
- Eventually, you will be able to reach the minimum project cost.
Try to tabulate these results as they will be easier to review.
Costs
Fixed costsThese are any costs that do not rely on the output. They could be rent, equipment payments, insurance, salaries of supervisors etc.
Direct costsThese are the costs that can be specifically identified with a particular project or program.
These could be salaries, fringe benefit, equipment, supplies, travel, training, consultancy fees, interest on loans, lease charges etc.
They may be specified in the proposal budget.
These are over and above any fixed cost for a particular project and will vary depending the output of the task.
Hence, if the out put doubles the variable cost will double. This is not strictly true for our example as doubling the number of workers will not necessarily double the output.
Let us assume that each man costs £100 per day.
Each man can lay 300 bricks / day and we have 5 men and 9,000 bricks to lay.
The duration is 9000 / (300 x 5) = 6 project days.
Hence the variable direct costs (relevant only to this project) = 6 (days) x 5 (men) x £100 = £3000.
The total effort required = 6 (days) x 5 (men) = 30 man-days.
If we add 2 more men whose performance level is 200 bricks / day we might estimate the duration as 5 project days.
In other words, the duration has reduced from 6 to 5 days, a saving of 1 day.
The cost of employing a man is still £100 per day.
The duration of the task = 5 days and we now have 7 men.
Hence, the number of man days are = 5 x 7 = 35 man-days.
Each man-day costs £100.
Thus, the total cost = 35 x £100 = £3,500.
So, the extra cost in reducing the duration to 5 days = £3,500 - £3,000 = £500.
As we saved 1 day the daily cost penalty = £500 / 1 (day) = £500.
Hence, in summary it has cost £500 to save 1 day.
This indicates that reducing task durations requires a cost.
If we wished to save 2.5 or 3 days the cost would not be pro rata. This is because as we increase the labour resource we gradually get to a point where extra labour will make no difference. Hence, we end up with a trade off.
As durations go down the cost penalty per day goes up.
This cost penalty per day will vary according to the task.
Clearly, we will save on some costs by reducing the duration and completing the task that much quicker.
Overall project
The act of ‘crashing’ tasks on the critical path will reduce the overall project duration at a financial cost.
However, the very act of reducing the overall project duration will produce cost savings as well on fixed costs.
There will be a net benefit based upon:
Cost of implementing the project duration reduction – the cost savings.
At first the increased savings will outweigh the costs but there will come a point when the cost of duration reduction becomes too expensive and the overall effect is not a benefit but a loss. If you were to plot a graph of ‘benefit’ versus ‘project duration’ there will be an optimum cost benefit.
This optimum is unlikely to be at the point of minimum project duration.
For some projects time is paramount. This might be the case where security is a major issue.
In this situation, the cost may be irrelevant if the project can be ‘crashed’ to its minimum duration.
Under PRINCE2® 2009 [see ‘The Complete Project Management plus PRINCE2’] planning is covered by the Plans theme.
The purpose of the Plans theme is to facilitate communication and control by defining the means of delivering the products (the where and how, by whom, and estimating the when and how much).
[see Plans - Purpose]
A plan can only show the ultimate feasibility of achieving its objectives when the activities are put together in a schedule that defines when each activity will be carried out.
[See Plans - The PRINCE2 approach - Prepare the schedule]
Identifying the plan activities and dependencies for a schedule are also covered within this theme.
[see Plans - The PRINCE2 approach - Identify activities and dependencies]
PRINCE2® is a Registered Trade Mark of the Office of Government Commerce in the United Kingdom and other countries.

